[자료구조] 2. Tree : Binary Tree, Heap, BST

1. Terminology

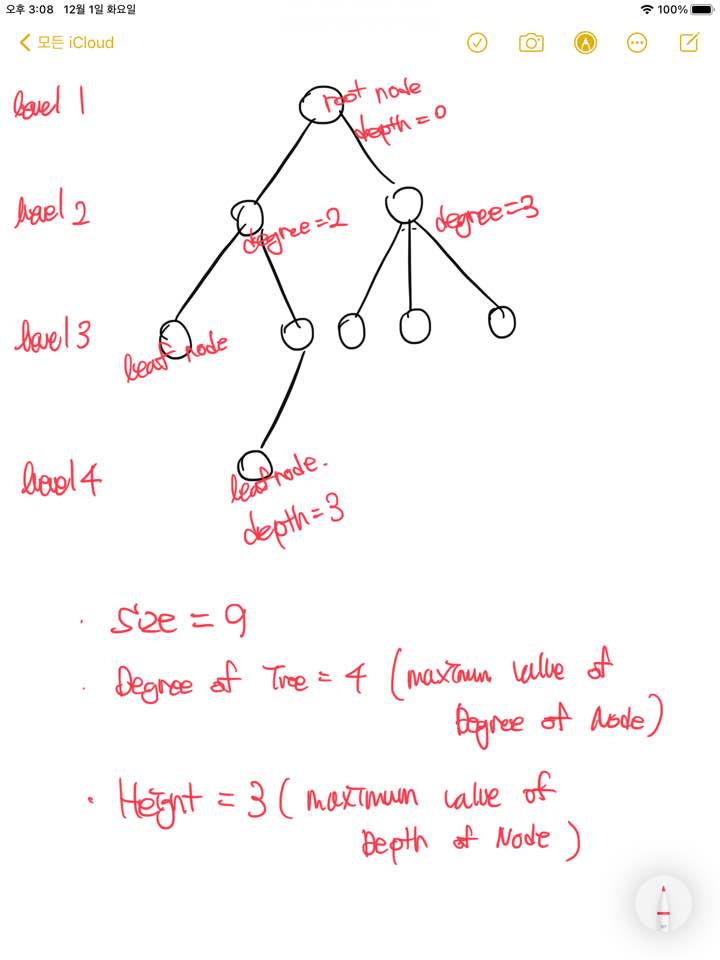
1) Degree : # of child the node has 2) Size : total # of node in tree

3) Depth : # of edge that need to pass from root node(>=0)

4) Height : maximum value of depth

5) Level : set of node at same level

 

 

2. Binary Tree

Tree의 각 Node가 최대 2개의 Children Node를 가지는 Tree 자료구조

 

* number of node in tree = n, height of tree = h 일때

→ 2h + 1 ≤ n ≤ 2^(h+1)-1

 

1) Compelete Binary Tree : 완전이진트리

마지막 level을 제외하고 모든 level이 완전히 채워져 있으며, 마지막 level의 모든 노드는 가능한 한 가장 왼쪽에 있도록 둔 Tree 자료구조

 

2) Threaded Binary Tree

- NULL link는 left-child일 때  inorder-processor node을 가리키고, right-childe일 때 inorder-successor node를 가리키는 Tree 자료구조

- 이 때의 NULL link를 Thread라 한다.

 

 

3. Heap

최대값 혹은 최소값을 찾아낸 연산을 최적화한 완전이진트리 자료구조

* priority_queue : heap 구조를 이용한 queue

* O(logN)

 

1) Insertion

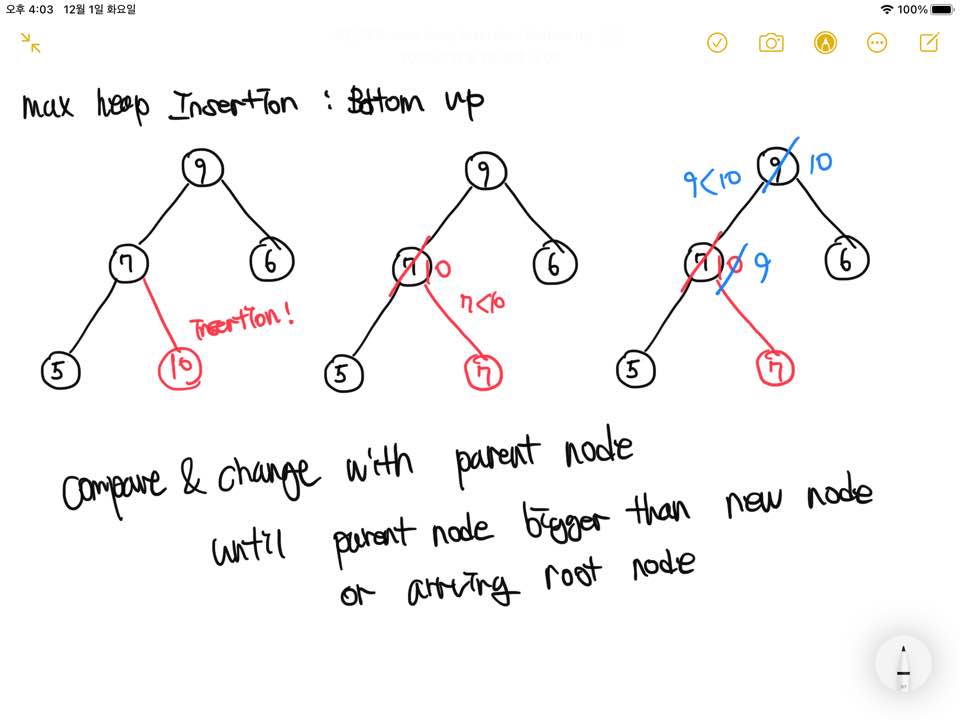
2) Deletion

 

 

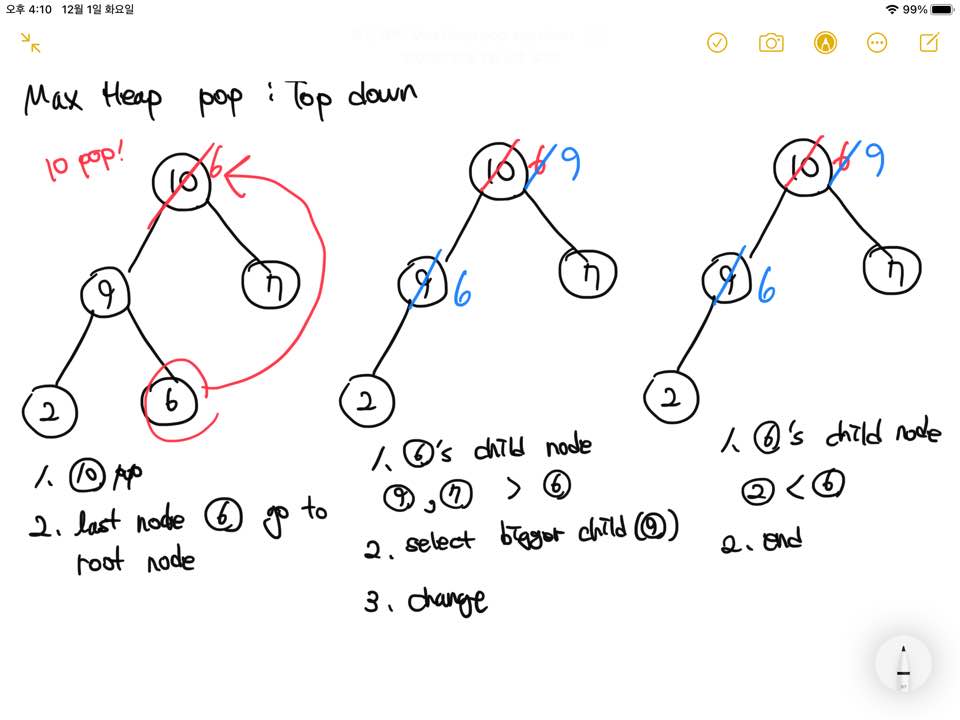
4. Binary Search Tree : 이진 탐색 트리

이진탐색의 효율적인 탐색 능력을 유지하고 삽입, 삭제 연산의 효율을 늘리기 위해 이진탐색(binary search)과 연결리스트(linked list)를 결합한 Tree 자료구조

 

* 완전이진트리는 아니기 때문에 Node가 한쪽으로만 치우친 경우 O(h)의 시간 복잡도를 가질 수 있다.

 

1) Property

- 중복되는 값을 갖는 노드는 없어야 한다.

- 각 노드의 왼쪽 서브트리의 노드는 해당 노드보다 작은 값을 갖는다.

- 각 노드의 오른쪽 서브트리의 노드는 해당 노드보다 큰 값을 갖는다.

- 트리 내 모든 서브트리도 이진 탐색 트리이다.

- 이진 탐색 트리를 Inorder traversal하면 정렬되어 출력된다.

 

2) Insertion

- Top-down으로 탐색하며 같은 값이 있을 경우는 return false;

- 적절한 위치를 찾았다면 원래 있던 노드의 parent와 연결하고

- 원래 있던 노드를 크기에 따라 삽입한 노드의 left 혹은 right child로 연결

 

 

3) Deletion

- 삭제할 값을 가진 Node 탐색

- 경우에 따라 3가지 방법으로 처리

case 1 : // no children
	
    free(node);
    
case 2 : // one child
	
    parent_node->left = node->left; // or right
    free(node);

case 3 : // both children
	
    tmp = t->right;
    
    while(tmp->left != NULL)
    	tmp = tmp->left; // tmp : node has maximun value in subtree
    
    t->data = tmp->data;
    t->right = deletion(tmp->data); // tmp를 위로 올렸으니 삭제해주어야 한다.

 

5.  Forest

하나 이상의 트리로 이루어진 disjoint set(서로소 집합)

각 트리를 하나의 root node로 묶으면 트리..